Predictability of a CD4 Count

Predictability of a CD4 Count

David Crowe

When an AIDS doctor declares that a patient with a CD4 count is “severely immunesuppressed”

he is making a prediction based on the CD4 count with near certainty. When

a doctor proclaims that an HIV positive person’s CD4 count of 200 or 350 or 500 shows

that it is “time to start drugs” they are also making a prediction on the basis of a CD4

count, a prediction with implied certainty. Perhaps, if pressed, the doctor might admit that

there are some people with low CD4 counts who are not sick, but the basic message is

that CD4 counts have been shown, scientifically, to be highly accurate indicators of your

stage of “progression to AIDS” – from asymptomatic to pre-AIDS (“AIDS-related

complex”) to full-blown AIDS and then death.

But, what is the evidence that CD4 counts are associated with stage of immune

suppression? And, how accurate would a prediction that a certain CD4 count indicates

that a person is at a particular stage of HIV or AIDS be?

Predictability of a CD4 Count

The World Health Organization states that HIV-positive people with no symptoms or

minor symptoms should start AIDS drugs when their CD4 count drops below 200

(cells/μL) and those with serious symptoms that don’t yet quality as AIDS should start

with CD4 counts under 350 (Guidelines for HIV diagnosis and monitoring of

antiretroviral therapy. WHO Regional Office for South-East Asia. 2009).

The US Department of Health and Human Services recommended, in 2001, that every

HIV-positive person with a CD4 count below 200 should take AIDS drugs, even if they

were in perfect health (Guidelines for the use of antiretroviral agents in HIV-infected

adults and adolescents. US Dept. of Health and Human Services. 2001 Feb 5). In 2008

they added an admittedly weaker recommendation that everyone with CD4 counts below

350 should also take AIDS drugs (again, regardless of current health) (Guidelines for the

Use of Antiretroviral agents in HIV-1-infected adults and adolescents. DHHS.

2008 Nov 3). In 2012 they added another recommendation, that they admitted was based

solely on opinion, not data, to take AIDS drugs no matter what CD4 count the patient had

(Guidelines for the Use of Antiretroviral Agents in HIV-1-Infected Adults and

Adolescents. NIH. 2012 Apr 12).

Normal Use of the Normal Distribution

I apologize, but we must talk about some basic statistical concepts…

Normally, in medicine, the normal distribution (or ‘Bell Curve’) is used to decide if two

groups are different, statistically speaking. In a simple medical example a clinical trial

could be run to compare blood pressure in a group of people taking a drug versus a group

taking a placebo or another drug. There will be variation, not everyone's initial situation

and reaction to the drug will be the same, so the blood pressures will form two bell curves

that will probably overlap quite a bit. The question that can be asked is whether the two

bell curves are statistically different. If they are then it can be concluded that the drug

worked. Technically the question that is asked is whether the two averages (approximate

centers of the curves known as means) are statistically different (with a certain assurance

or probability, usually 95% or 99%).

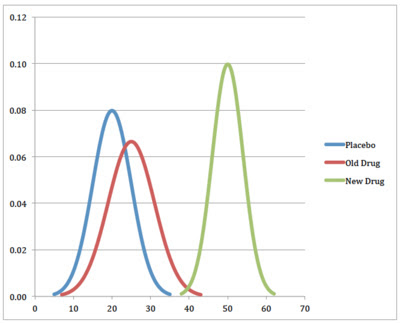
Let’s take an artificial example, a drug manufacturer’s dream, a trial of placebo (blue),

old drug (red) and new drug (green). The height of the curves represents the relative

portion of patients with each measured value of an important parameter that goes from

left (bad) to right (good) across the bottom. Your eye can see, and statistics would verify,

that the red and blue curves are not distinctly different (i.e. the old drug is not very

effective) but that the green curve is distinctly different (i.e. the new drug works).

Normal distributions are characterized by two parameters: the value of the data at their

peak (known as the average or mean and having the values 20, 30 and 50 for these three

curves) and also by a measure of their wideness, known as the standard deviation. A

perfect normal distribution will have about 68% of the data within (i.e. plus or minus)

one standard deviation of the mean, about 95% within two standard deviations and over

99% within three standard deviations. A normal distribution with a large standard

deviation indicates a population with more variability.

In the example above, the green (new drug) curve has the smallest standard deviation and

therefore the most predictive value. If the experimental results held in the real world, the

new drug would produce values of the measured parameter between 40 and 60 in a large

majority of people, a narrower range than found in the people not taking anything

(placebo) or the old drug.

Normal Distributions and CD4 Counts

The practice of using CD4 counts to determine what stage of AIDS someone is at (e.g. in

the United States a CD4 count under 200 is considered AIDS even if no AIDS-defining

illnesses are present) and to determine when to start drugs implicitly contains an

assumption that a CD4 is an accurate indicator of disease stage.

Considering the graph above, what if, instead of giving people drugs or placebo and

monitoring for some lab number, you took that lab number and tried to predict whether

they were taking the drug or not? A reading of 20 would indicate that someone was not

likely in the green group, but could be in either the red or blue group. A reading of 50

would imply a very high probability that someone was in the green group but a reading of

40 would have a very high level of uncertainty about which group they were in. This

doesn’t seem very useful unless we are trying to determine if someone is really taking the

drug they were prescribed, but what if the three curves indicated disease stages and we

wanted to use the current value (20, 40, 50 etc.) to determine how sick someone was?

For example, what if the curves represented CD4 counts of people at different stages of

HIV infection?

What would the predictive power of a CD4 count be if we wanted to guess which stage of

“HIV disease” someone was in (HIV-negative, recently infected, HIV-positive

asymptomatic, AIDS) like ‘real’ AIDS doctors do routinely? If we had an estimate of the

normal distributions for these stages the mathematics would actually be quite simple –we

would just take the height of any one normal distribution curve at any point and divide it

by the height of all the curves at the same point to estimate the probability.

As an example, with the curve above, if the heights of blue, red and green for the value of

20 are 0.08, 0.06 and 0.001 the probability of someone with a reading of 20 being in the

blue group is 57%, the probability of red is 43%, and the probability of being in the green

group is less than 1%. Since the heights for a value of 40 are 0.001, .003 and .005, the

probabilities of blue, red and green are 11%, 33% and 56%. Clearly, with a value of 40 it

is impossible to guess which group this person is in.

Similar data on CD4 counts is surprisingly hard to obtain. I have shown in two previous

analyses that most published graphs on CD4 counts are imaginary, mostly derived from

the feverish mind of Anthony Fauci:

• Text – http://aras.ab.ca/articles/scientific/DatalessGraphs.html

• Video – http://vimeo.com/26441488

But one paper does appear to show a time series, a series that we will examine in detail.

Real Data

A paper from 1989 (Lang W et al. Patterns of T lymphocyte changes with human

immunodeficiency virus infection: from seroconversion to the development of AIDS. J

Acquir Immune Defic Syndr. 1989; 2(1): 63–9) is the only one that I know of that not

only show CD4 counts, but CD4 counts over time and stage of “HIV disease”. It certainly

has its problems, among them:

• The use of Standard Error of the Mean (SEM) underestimates the variation in the

data by a large factor.

• The different groups of measurements were from three different groups of people.

But, putting the limitations aside, here is the data that was presented.

One of the advantages of this paper is that from the graph, the two parameters of the

normal distribution, mean and standard deviation, can be calculated. The mean is simply

the height of the short horizontal line in the middle of each datum and the standard

deviation is the SEM multiplied by the square root of the sample size (“Number of

Participants”, conveniently provided). This means that every point in time provides its

own normal distribution.

When we convert the SEM to the actual 95% confidence interval for the data (an estimate

that 95% of the data is within the shown line) you can start to see the problem with trying

to predict HIV/AIDS stage from the CD4 count:

But, even so, it would appear that a CD4 count of 200 would rule out someone being a

recent HIV seroconverter since none of the 95% confidence intervals stretch that far.

Here is the question we should ask: Given a specific CD4 count, what is the probability

that the person is a recent HIV seroconverter, AIDS-free long-term seropositive, a

recently diagnosed AIDS patient or HIV-negative (the paper also provides some

reference data not shown on this graph)? Our technique will be to estimate the fraction of

the probability provided by each normal distribution (starting with the HIV-negative data,

3 months before seroconversion, and so on up to 1 month after AIDS diagnosis) and then

sum them for each of the four groups. We will look at the probability for a CD4 count of

200 (automatic “AIDS” in the United States), 350 (another common point below which

therapy is started), 500 (taken to be the bottom of the normal range) and 1000 (well into

the normal range).

What we get is the following:

Note: A spreadsheet with the calculations is available as an Excel or PDF file.

What this means is that even with a very low CD4 count our ability to predict disease

stage is poor. That is, if someone has a CD4 count of 200, they might be a recent

seroconverter, a long-term asymptomatic or an AIDS. And even the 8% probability that

they are HIV-negative is not insignificant.

If a perfectly healthy person has a false positive HIV-test (assuming that there is such a

thing as a true positive) the data in this study (average CD4 count of 1080 with standard

deviation of 480 derived from SEM of 20 with sample size of 577) shows that

approximately 11% of these people would have a CD4 count below 500 (and might be

put on AIDS drugs) and 3.4% would have a CD4 count below 200 (and would certainly

be put on AIDS drugs). If these results hold for the general population and all 300 million

HIV-negative people in the US were tested it would be concluded that about 33 million

were “immune suppressed” and about 10 million would be called “severely immunesuppressed”.

What

this

Means

This simple statistical analysis shows that CD4 counts are useless at determining what

disease stage someone is at – unable to distinguish between those recently diagnosed with

no symptoms and those with actual AIDS. It is therefore absurd for AIDS doctors to hold

these counts in such esteem that, in the absence of any evidence of opportunistic

infections (clinical immune suppression), they talk about people with HIV-positive

people with CD4 counts below 200 as “severely immune-suppressed” and use the counts

to coerce people to start toxic antiretroviral therapy.